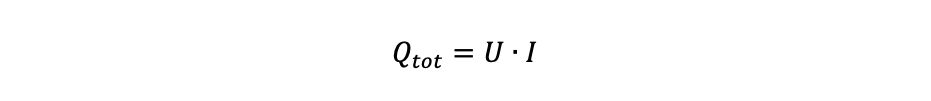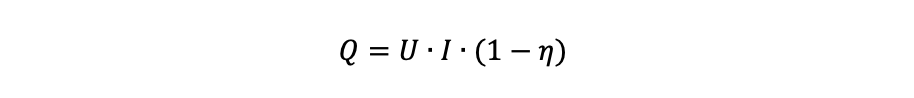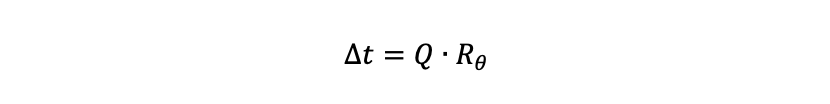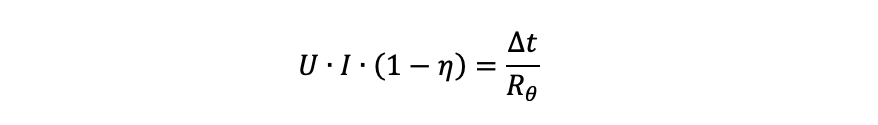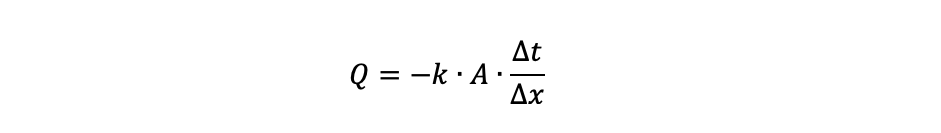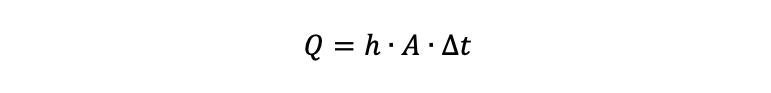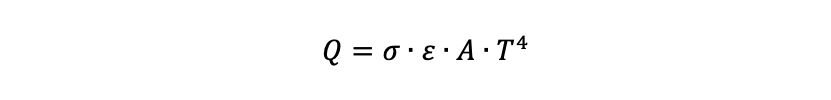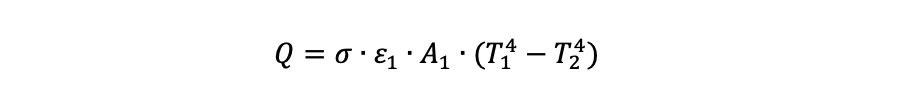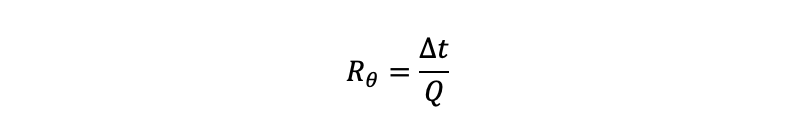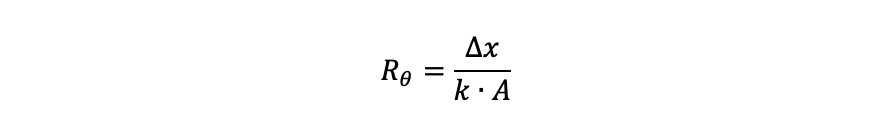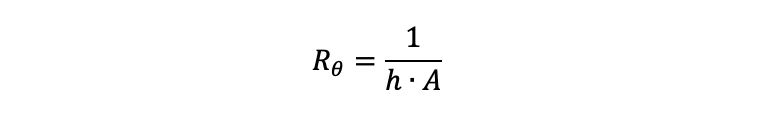Det första och mest fundamentala faktum som rör elektronikkylning och som vi behöver känna till är detta: All elektronik genererar värme.

 

Elektroner som rör sig genom material möter motstånd och genererar därigenom värme, jämförbart med mekanisk friktion. Ju högre elektrisk effekt som passerar genom materialet, desto större blir också värmen som genereras. Den elektriska effekt som godtycklig enhet matas med — oavsett om det är en hel apparat eller en enskild komponent – är:

Där Q_tot är den totala effekten [W], U är spänningen [V], och I är strömmen [A].

 

Den effekt som används för att åstadkomma önskad output från en enhet definieras av dess verkningsgrad, η. Resten, 1–η, är förlust, och går ut som värme.

 

Således är den förlusteffekt som genereras i enheten:

I varje tillämpning måste kyllösningen kunna avge denna mängd värme, annars ackumuleras värmen i form av förhöjd temperatur. Den sista bisatsen i föregående stycke är avgörande för att förstå värme: ”värme ackumuleras i form av förhöjd temperatur”.

 

Det är vanligt att tänka på värme som temperatur, men i själva verket är temperatur en följd av värme – ansamlad termisk potential, om man så vill. Värme förflyttas från hög temperatur till låg temperatur – från varmt till kallt. Värme kan endast glida ner en termisk gradient på det sättet. Om det inte finns någon termisk gradient – ingen potentialskillnad – rör sig heller inte värmen. Hur brant gradientens lutning måste vara för att värmen skall förflyttas längst den beror på den termiska resistansen i det medium som värmen skall röra sig genom.

 

Om det inte finns någon temperaturskillnad, men det finns en värmekälla – dvs. en termisk effekt – kommer effekten att ackumuleras som en höjd temperatur vid den punkt där den genereras, tills det blir en temperaturskillnad, och vidare tills gradientens lutning blivit tillräckligt brant för att värmen ska ”glida” längst den i samma takt som den genereras igenom befintlig resistans.

 

Denna korrelation låter sig beskrivas enligt följande:

Där Δt är temperaturskillnaden mellan värmekällan och omgivningen [K eller °C], är Q den termiska effekten [W] – i de flesta fall identiskt samma värmeeffekt som den som genereras i den tidigare formeln – och R_θ är det termiska motståndet [K/W]. Denna energibalans – och dess konsekvens – är viktig att förstå: värme in kommer alltid att vara lika med värme ut. Det är bara en fråga om hur varm värmekällan behöver bli för att värmen skall kunna avges i samma takt som den genereras. Således kan vi arrangera om och slå ihop de två sista formlerna:

Δt, som alltså är lika med värmekällans temperatur minus omgivningstemperaturen, bestämmer vilken temperatur vi i slutändan får i komponenterna (här förenklar vi bort t.ex. instrålad värme från omgivningen). Om vi ​​vill hålla den så låg som möjligt kan vi antingen minska input – vänster sida av ekvationen — genom att använda mindre effekt och/eller använda komponenter med högre verkningsgrad, eller minska den variabel som vi har kvar på outputsidan: det termiska motståndet. Mer om detta i fjärde avsnittet.

 

På partikelnivå är värme vibration – molekyler och atomer som vibrerar. Mata in energi i en sådan partikel, och den kommer att lagra denna energi i form av en ökad vibrationsfrekvens. Ju högre frekvensen är, desto högre är den termiska potentialen, dvs. temperaturen. Ingen vibration alls är liktydigt med ingen temperatur – dvs. absolut noll (0K eller –273,15°C). Denna vibration kan överföras mellan partiklar genom tre fysiska mekanismer: ledning, konvektion och strålning.

Del II – Konduktiv och konvektiv värmeöverföring

Ledning är värmeöverföring i fasta material eller stillastående fluider (en ”fluid” inom fysik avser godtycklig vätska eller gas). Det handlar enkelt uttryckt om att vibrationen i en partikel smittar av till närliggande partikel, och sedan till nästa, och nästa och så vidare. Detta kan också beskrivas i Fouriers lag.

 

Ledning beskrivs matematiskt av Fouriers lag, enligt följande:

Där Q är den termiska effekt som förs genom materialet [W], A är ledarens tvärsnittsarea [m²], Δt är temperaturskillnaden över materialet [K eller °C], och Δx är ledarens längd [m]. Detta lämnar k, som är materialets termiska konduktivitet [W/(m·K)].

 

Den termiska konduktiviteten är en materialegenskap som beskriver hur lätt värme leds genom materialet i fråga. Det är en bulkegenskap, vilket innebär att det – givet ett isotropt material – alltid kommer att vara konstant, oavsett geometri. Anisotropa kroppar (som t.ex. en PCB) kan dock ha olika konduktivitet i olika riktningar.

 

Skalan för termisk konduktivitet sträcker sig från 0,02W/(m·K) för stillastående luft, genom 0,2 för de flesta polymerer, cirka 16 för rostfritt stål, runt 200 för typisk aluminiumextrusion, 398 för koppar, upp till cirka 2 000W/(m·K) för diamant och slutligen grafen, som kan ha en konduktivitet i plan på upp till 5 000W/(m·K), beroende på vem som mäter det och hur.

Konvektion

Konvektion inträffar när nästa partikel i kedjan som fångar upp vibrationen inte längre är låst av sina grannar utan är fri att sväva iväg. På så sätt bär den vibrationen – dvs. den termiska ”laddningen” – med sig. Den kan sedan träffa på en annan partikel någon annan stans, till vilken den då kan överföra sin värme genom ledning.

Den konvektiva värmeöverföringen från en yta till en omgivande fluid beskrivs av Newtons regel:

Där Q fortfarande är överförd termisk effekt [W], A är konvektionsytans area [m²], och Δt är temperaturskillnaden mellan ytan och den omgivande vätskan [K eller °C]. Variabeln h är värmeöverföringstalet [W/(m²·K)].

 

Värmeöverföringstalet beror på ett mycket stort antal faktorer, inklusive (men på intet sätt begränsat till) konvektionsmekanism (naturlig eller forcerad konvektion), konvektionsytans geometri (vertikal platta, horisontell cylinder, insidan av ett cylindriskt rör etc, etc), konvektionsfluid (luft, vatten, mineralolja etc), och karakteristiken på flödet över ytan (snabb, långsam, laminär, turbulent etc).

 

Värdet på h kan typiskt sträcka sig från låga ensiffriga tal för naturlig konvektion i luft till flera tusen för forcerad konvektion i vatten – och ytterligare mycket högre, om fasändring (kokning) förs in i ekvationen.

Del III – Radiativ värmeöverföring

Dessa varma – vibrerande – partiklar avger också vågor i form av elektromagnetisk strålning i takt med sin vibration. Ju högre vibrationsfrekvens – dvs. temperatur – desto högre frekvens – dvs. kortare våglängd – har strålningen. När denna strålning träffar en annan partikel kommer den partikeln att fånga en del av vågens energi, något liknande resonans i föremål som träffas av ljudvågor.

 

Den lägsta kända temperaturen i naturen är den kosmiska bakgrundsstrålningen vid 2,7K som toppar vid cirka 1mm våglängd – den allra översta änden av EHF-radiobandet. Typiska omgivningstemperaturer på jordens yta är runt 300K, som toppar vid cirka 10μm, dvs långvågigt infrarött, medan ytan av vår sol vid 6 000K toppar vid cirka 500nm, vilket är mitt i spektrumet av synligt ljus. Vissa supernovor värmer upp sina gaser till uppemot 55 000 000K, som toppar någonstans i nanometerregionen, dvs. röntgenstrålning.

 

Matematiskt beskrivs värmestrålningen från en kropp av den bedrägligt enkla Stefan-Boltzmanns lag:

Men värmeavledning genom strålning är något komplicerad att beräkna, för det första på grund av att det rör sig om ett värmeutbyte – eftersom alla kroppar utstrålar värme, innebär det att medan en kropp avger värme kommer den samtidigt också att ta emot värme från sin omgivning – och för det andra på grund av att utbytet är avhängigt en lång rad geometrifaktorer.

 

Men om vi kan anta att den studerade kroppens yta är mycket mindre än omgivningens yta och att denna omgivning har en mer eller mindre enhetlig temperatur, kan nettoutbytet förenklas enligt följande:

Där T₁ är den absoluta yttemperaturen för den emitterande kroppen [K], T₂ är den absoluta yttemperaturen för den omgivande miljön [K], A₁ är den totala ytan för den emitterande kroppen [m²] och σ är Stefan-Boltzmanns konstant [~5,7·10^-8W/(m²·K⁴)]. Den slutliga variabeln ε₁ är den strålande ytans emissivitet.

 

Emissivitet representerar en ytas effektivitet med avseende på att avge sin termiska energi som strålning. Den är ett värde mellan 0 och 1, där 1 representerar en ideal svartkropp. För de flesta ogenomskinliga fasta material är ε även lika med α, absorptiviteten, vilket är en ytas förmåga att absorbera termisk energi som den träffas av. Värdet är också beroende av temperaturområdet, dvs strålningens våglängd. Således kan en yta mycket väl t.ex. ha en struktur som är utstrålande i infrarött, samtidigt som den har en färg som reflekterar den synliga värmestrålningen från solen.

 

När vi studerar formlerna för ledande, konvektiv och radativ värmeöverföring är det värt att notera att vissa parametrar återkommer i samtliga. En är temperaturskillnaden. I samtliga formler är det uppenbart att ju större temperaturskillnad som finns i systemet, desto mer värme kommer att flöda.

 

Ännu mer intressant är dock observationen att arean är en viktig faktor i alla tre formler. Ju större yta, desto bättre värmeöverföring – med andra ord, om vi kan ha större ytor kan vi minska temperaturskillnaden för en given termisk effekt. Detta är viktigt för kylning, eftersom värmekällans – dvs. komponentens – temperatur i slutändan kommer att vara lika med den temperaturskillnad som läggs till ovanpå den omgivande temperaturen.

 

Vi kan alltså börja dra slutsatsen att ökning av arean – värmespridning – kommer att vara en nyckeluppgift i all termisk design.

Del IV — Beräkning av termisk budget

Medan Fouriers lag, Newtons regel och den förenklade Stefan-Boltzmanns lag är användbara verktyg, tenderar de flesta approximeringar på lägre nivå istället att förlita sig på termisk resistans. Enheten för termisk resistans är K/W eller °C/W. Det vill säga, hur många grader kommer temperaturen att öka över motståndet per watt termisk energi som överförs genom den. Vi har redan berört en definition av termisk resistans:

Det är i viss mening analogt med Ohms lag, där elektrisk resistans är lika med spänning över ström. Det är detsamma här: resistansen är lika med potentialen över flödet. Om vi pluggar in Fouriers lag i denna formel kan vi komma fram till en definition av termisk resistans för konduktiv värmeöverföring:

För konvektiv värmeöverföring kan vi istället plugga in Newtons regel och komma fram till följande:

Med en lämplig justering av h-värdet är denna formel faktiskt användbar även för de kombinerade effekterna av konvektiv och radiativ värmeöverföring, eftersom dessa vanligtvis förekommer samtidigt.

 

Dessa formler möjliggör beräkning av termisk resistans för de flesta komponenter i en värmeöverföringskedja, helt enkelt genom att plugga in kända geometrier och materialdata i formlerna. Det noteras att den termiska resistansen är ett applikationsspecifikt värde – den beror på geometrier och andra specifika omständigheter som inte nödvändigtvis kan överföras till andra applikationer.

 

Termisk resistans är bekväm att använda, eftersom motstånd i en värmeöverföringskedja – antingen empiriskt bestämd, beräknad eller avläst från datablad – enkelt kan adderas på samma sätt som elektriska resistanser. En junction-to-case-resistans från ett komponentdatablad kan således adderas till den beräknade resistansen för en termisk interface-pad, till vilken en termisk resistans för en kylfläns kan adderas från ett annat datablad, för att ge en grov aning om var junction-temperaturen kan förväntas landa vid en viss given förlusteffekt och omgivningstemperatur.

 

Även om termisk resistans på många sätt är analogt med Ohms lag, är analogin också begränsad — Ohms lag beskriver endimensionellt flöde, men värme rör sig tredimensionellt. Icke desto mindre låter sig många problem förenklas till en dimension, då lagen också blir tillämpbar.

 

Det är värt att understryka ytterligare en gång – såsom framgår av formlerna ovan – att area är en nyckelfaktor för låg termisk resistans. Därför är spridning av värmen så mycket och så tidigt som möjligt i värmeöverföringskedjan ofta avgörande för framgångsrik termisk design.

Del V — Utmaningen framåt

Elektronikhårdvara utvecklas idag i tre väldigt tydliga riktningar – och detta gäller oavsett vilken typ av elektronik vi betraktar:

• Miniatyrisering: Komponenter och apparater blir allt mindre och mer kompakta.
• Förmåga: Enheter kör större och mer krävande programvara och utför fler operationer parallellt.
• Hastighet: Digitala kommunikationshastigheter ökar, liksom busshastigheter och läs-/skrivhastigheter i lagringsenheter etc.

Alla dessa utvecklingstrender har en mycket viktig sak gemensamt: de driver förlustvärme.

 

Miniatyrisering ökar effekttätheten. När en enhet görs mindre kommer värmekällorna i den – ledare, komponenter, alla platser där elektroner stöter på motstånd – närmare varandra.

 

Mer kapabla enheter förbrukar oundvikligen mer effekt, eftersom ju mer de gör – ju fler elektroner som rör sig – desto mer effekt går åt. Följaktligen genererar de också mer förlustvärme.

 

Hastighet inom elektronik är en fråga om att flytta fler datapaket under en given tid. Varje datapaket är enkelt uttryckt en knippe elektroner — och återigen, fler paket motsvarar fler elektroner, motsvarar mer värme.

 

Nettoeffekten är att termiska problem inte endast ökar i branschen; de eskalerar i en exponentiell takt! Förvisso kan tillkomsten av nya, effektivare halvledarmaterial med mindre elektriskt motstånd och bättre kunskap om effektiv design kunna motverka dessa trender, men historiskt varje höjning av designtaket som vunnits genom förbättrad verkningsgrad alltid tagits i anspråk för höjd prestanda. Den termiska baselinen har således oförändrat befunnit sig på en maxnivå.

 

Termisk design är därför en mycket viktig faktor för elektronikindustrin. Vår förmåga att leverera hårdvara och de prestandanivåer som våra respektive marknader kräver är helt beroende av vår förmåga att utforma termiska lösningar som kan leverera den verkningsgrad, kostnadseffektivitet och formfaktor som krävs.

 

Jussi Myllyluoma
Cool Sweden Initiative

Expertisen inom elektronikkylning träffas på Cool Sweden Workshops 2024

Den 7 maj samlas expertisen inom Thermal Management på Stockholmsmässan för en dag med workshops och föreläsningar inom det heta ämnet elektronikkylning. Som deltagare får du kunskap om den senaste tekniken inom Thermal Management och elektronikkylning. Du får möjlighet att diskutera med presentatörer, utställare, demopartners och övriga deltagare. Du träffar rätt människor, i rätt sammanhang.

 

Välkommen till Cool Sweden Workshops 2024!